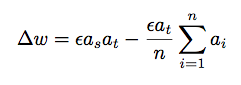Subtractive Normalization

Hebbian learning rules suffer from the fact that weights tend to achieve maximum or minimum values. Several variants of Hebbian learning have been introduced to address this issue; Subtractive Normalization is one of them.

Subtractive normalization is a form of Hebbian learning where the sum of the weights attaching to a given neuron is kept relatively constant. This is achieved by subtracting the product of the target neuron activation a_t and the average activation of source neurons a_i attaching to a_t:

In order for the effect of keeping the sum of the weights attached to a neuron constant, those weights must all use this rule.

The strength of this synapse is clipped so as to remain between the lower and upper bounds specified for this synapse. Note that clipping the values of this type of synapse could interfere with its intended effect of keeping the sum of weights attaching to a neuron constant.

Note that although this method constrains the sum of the weights to some fixed number, it allows for some weights to go off to positive infinity while others are going off simultaneously to negative infinity.

See Peter Dayan and Larry Abbott, Theoretical Neuroscience, Cambridge, MA: MIT Press, p. 290. 

Also see K. Miller  and  D. MacKay, "The Role of Constraints in Hebbian Learning", Neural Computation 6, 120-126 (1994).

Learning Rate

The learning rate ε.