Spike Responders

In Simbrain all action potentials are modelled as Dirac delta functions, (the Dirac delta function is 1 at exactly 0 and 0 for all other values on [-∞, ∞]). This just means that they are instantaneous in time and that insofar as the neuron that emitted the spike is concerned no spike is more or less powerful than another. However, this is problematic because everything takes some amount of time, and so spike responders exist as a generic term for any function which assigns a temporally extended value to an instantaneous pre-synaptic spike. Generally speaking (and by default) all synapses originating at a spiking neuron have a spike responder and use that spike responder to determine how strongly they should impact their target neuron.

The top right neuron in the image here shows a spike responder in action. When the neuron that connects to it spikes, the spike responder produces a 1 which then decays to zero (see Jump and Decay).

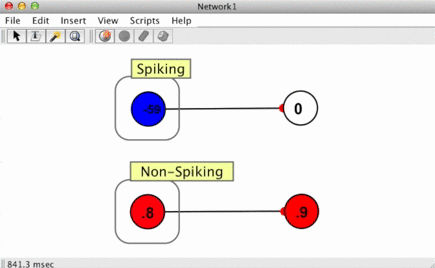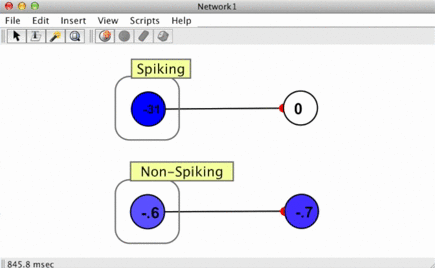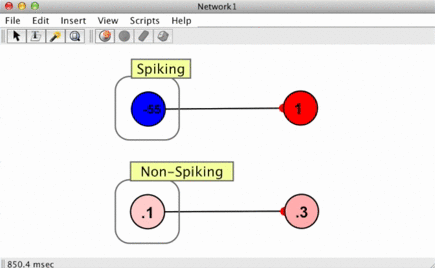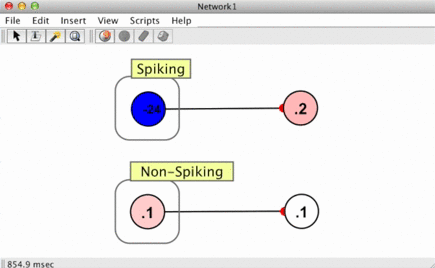
In biological settings, when a spike arrives at a post-synaptic cell (the target neuron of the spiking neuron), a "wave" of activation is created. This is modeled using a "response function" which characterizes a synaptic current, the influx of chemicals into a target cell which occurs when vesicles are released from a source neuron. In more formal terms (most) spike responders perform a convolution of some function and the Dirac delta function representing spikes.

The input to a neuron using the synaptic input type uses the post synaptic response as determined by the impinging synapses' post-synaptic response, as determined by the spike responder. This input takes many forms depending on the neuron type of the post-synaptic cell, but the general form of the input equation is as follows:

$$ x_{syn} \;=\; \sum\limits_{j = 1}^N PSR_j(\Delta_{spk}, w_{j}) $$

Where $x_{syn}$ represents either pure synaptic current, the conductance (or fraction of open ion channels of a given type), or net input depending on the target neuron. $PSR_{j}$ is the post synaptic response of synapse j as determined its the spike responder. The spike responder determines the PSR using two variables: $\Delta_{spk}$ or the time since the last spike of the pre-synaptic neuron, and $w_{j}$, the absolute synaptic efficacy (also known as the "strength" or "weight") of the impinging synapse.

In sum, what is passed on to the post-synaptic neuron is the value of the response function scaled by the strength of the weight. That being said, there are a number of unique response functions that dramatically change the utility of the spike interaction. The response function can be thought of as the wave form of the response to a spike.