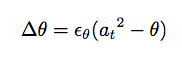Hebbian Threshold
This is a variant of Hebbian learning in which the learning rate is proportional to the difference between the post-synaptic activation at and a threshold θ, where θ can be fixed or sliding.
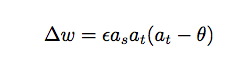
If θ is set to be sliding, then it changes at each time step by its own learning rate times the difference between the square of the post-synaptic activation and its current value. If θ is fixed, it will not change according to the proceding function, and will remain as it was left.
The rule seems to work best for small activation and weight values (between 0 and 1).
This rule is also known as the BCM rule (Bienenstock, Cooper, and Munro).
See Peter Dayan and Larry Abbott, Theoretical Neuroscience, Cambridge, MA: MIT Press, pp. 290-291.
Also see the Scholarpedia article on BCM Theory.
Learning Rate
This value changes the rate of the change of the synapse, denoted by epsilon in the equation above.
Threshold
The "output threshold" value the output activation at has to be above in order for the weight to increase.
Threshold Momentum
The value that scales the rate of the change of this synapse, denoted by ε above.
Use Sliding Output Threshold
If this is set to yes, then the threshold θ will change according to the equation above; otherwise it stays fixed.