Additive
These neurons were developed for use in the continuous version of Hopfield networks. They were intended to be broadly biologically plausible. Their dynamics are similar to several other neurons, including the Naka Rushton, IAC, and decay neurons, in that the activation value will decay towards a steady state determined by the weighted inputs W to the neuron.
Activation is computed by integrating the following differential equation using Euler's method:
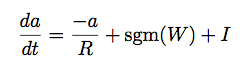
The resistance R functions essentially a time-constant. I is the external input to the neuron. W is the weighted inputs without external input (which is added separately). "sgm" is the sigmoidal function described by Hopfield in his original article: sgm(x) = 2/ π * arctan(π * λ * x) / 2 .
See Simon Haykin (2002), Neural Networks, section 14.5.
Time step
See time-step.
Lambda
This controls the slope of the sigmoidal. Bigger λ = steeper slope, approaching a step function as λ increases.
Resistance
Like a time constant. Make it larger and things slow down; make it lower and things speed up.
Use Clipping
See clipping.
Add Noise
If this is set to true, random values are added to the activation via a noise generator. For details how the noise generator works, click here.