Naka-Rushton Neuron
With this activation function, weighted inputs to a neuron are interpreted as stimuli intensities and the activation of the neuron is interpreted as a spike rate. For standard values of its parameters there is a gradual increase in firing until the neuron fires near its maximum rate.
The activation of this type of neuron will tend to follow a value S(W) which is defined as:
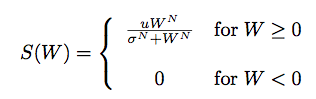
In this equation W is weighted inputs, u is upper bound (which here represents maximum spike rate), N is steepness, and sigma is the semi-saturation constant. This is roughly a sigmoidal function with a lower asymptote of 0 and an upper asymptote of u. This is realistic because the number of times a neuron fires in an interval of time is always non-negative.
The way in which the activation value a is made to follow S(W) is by making S(W) the fixed point of the simple differential equation:
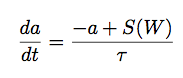
The time constant τ controls the rate at which activation tends toward the fixed point.
Adaptation
If useAdaptation is set to true, then the activation (spike rate) will tend towards zero. This models "spike rate adaptation," according to which neurons have finite resources which prevent them from rapidly spiking indefinitely.
Adaptation is modeled by adding an adaptation variable A, which increases the steepness of the sigmoidal-like function S by increasing the semi-saturation constant, and thereby moving the fixed point of the activation function towards its minimum value.
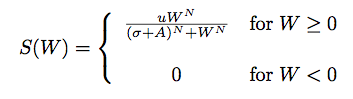
A is a function of the activation of the neuron:
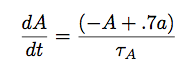
So the neuron will "adapt" more rapidly when it is firing more. Adaptation is controlled by its own time constant, τA, which should be much larger than τ, so that the adaptation will occur more slowly than the overall evolution of the firing rate.
The value of A can be observed via the tool tip on a neuron's graphical representation.
Both differential equations are implemented by integrating a differential equaton using the Euler method. The time-step of the Euler method is a global variable.
See Hugh Wilson, Spikes, Decisions, and Actions, Oxford: Oxford University Press, pp. 19-22, and 81-82.
Steepness
This value, denoted by N above, controls the steepness of the sigmoidal-like function S(W).
Semi-saturation constant
This value, denoted by sigma above, is the point at which S(W) reaches half of its maximum value. It affects both steepness and the location of the inflection point. For small values of sigma, S is approximately a step function; for large values the function becomes less steep and the location of the inflection point increases.
Time constant
This value, denoted by τ above, controls the rate at which the activation tends to the fixed point S(W).
Add Noise
If this is set to true, random values are added to the activation via a noise generator. The random values are added after the activation is computed. For details how noise generator works, click here. TODO: Revisit computation of this relative to time-step.
Use Adaptation
If this is set to true, spike rate adaptation (described above) is utilized.
Adaptation Parameter
The parameter of spike rate adaptation.
Adaptation Time Constant
This value, denoted by τA above, controls the rate at which the adaptation variable tends to its minimum value.