Izhikevich Neuron
The Izhikevich model neuron was developed as an efficient, powerful alternative to the integrate and fire model. The model uses two variables, a variable representing voltage potential and another representing membrane recovery (activation of potassium currents and inactivation of sodium currents).
To explore this neuron, you can use the script spikingNeuronDemo.bsh, from the workspace script menu.
This is a spiking neuron, so when the voltage passes a threshold value a spiking event occurs, the GUI neuron turns yellow, and the voltage and recovery variable are reset.
Since a is a parameter of the model, we use v to represent activation (voltage potential). u represents the recovery variable. Voltage is computed by integrating the following two differential equations using Euler's method:
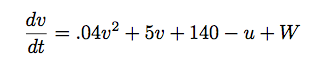
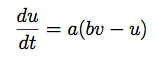
W is weighted inputs; a and b are abstract parameters of the model.
When the voltage exceeds a threshold value, which is preset at 30, both v and u are reset, as follows:
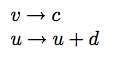
Thus there are four parameters for this system. According to Izhikivech, "The model can exhibit firing patterns of all known types of cortical neurons with [a suitable] choice of parameters"
Links / References
Izhikevich's page discussing this model.
Eugene Izhikevich (2004), "Which Model to Use For Cortical Spiking Neurons," IEEE Transactions on Neural Networks.
Parameters
Time step
See time-step (Izhikevich uses .2 in his paper.)
A
Parameter for recovery variable.
B
Parameter for recovery variable.
C
The value for v which occurs after a spike.
D
A constant value added to u after spikes.
Ibg
Constant background current.
Add Noise
If this is set to true, random values are added to the activation via a noise generator. For details of how the noise generator works, click here.
Some useful Parameter Settings
(See link above for more information)
| A | B | C | D | I (Input ) | |
| Tonic spiking | 0.02 | 0.2 | -65 | 6 | 14 |
| Phasic spiking | 0.02 | 0.25 | -65 | 6 | 0.5 |
| Tonic bursting | 0.02 | 0.2 | -50 | 2 | 15 |
| Phasic bursting | 0.02 | 0.25 | -55 | 0.05 | 0.6 |
| Mixed mode | 0.02 | 0.2 | -55 | 4 | 10 |
| Spike frequency adaptation | 0.01 | 0.2 | -65 | 8 | 30 |
| Class 1 | 0.02 | -0.1 | -55 | 6 | 0 |
| Class 2 | 0.2 | 0.26 | -65 | 0 | 0 |
| Spike latency | 0.02 | 0.2 | -65 | 6 | 7 |
| Subthreshold oscillations | 0.05 | 0.26 | -60 | 0 | 0 |
| Resonator | 0.1 | 0.26 | -60 | -1 | 0 |
| Integrator | 0.02 | -0.1 | -55 | 6 | 0 |
| Rebound spike | 0.03 | 0.25 | -60 | 4 | 0 |
| Rebound burst | 0.03 | 0.25 | -52 | 0 | 0 |
| Threshold variability | 0.03 | 0.25 | -60 | 4 | 0 |
| Bistability | 1 | 1.5 | -60 | 0 | -65 |
| DAP | 1 | 0.2 | -60 | -21 | 0 |
| Accomodation | 0.02 | 1 | -55 | 4 | 0 |
| Inhibition-induced spiking | -0.02 | -1 | -60 | 8 | 80 |
| Inhibition-induced bursting | -0.026 | -1 | -45 | 0 | 80 |