Simbrain > Network > Subnetwork > Standard Network

Echo State Network

Echo state networks (ESNs) are a class of recurrent neural networks (RNNs) which arose from the need for simpler (and more efficient) training algorithms for RNNs. Together with its cousins the Liquid State Machine and later Backpropagation Decorrelation Networks, ESNs lie within the umbrella category of Reservoir Computing. Networks within this category (including ESNs) are generally characterized by a sparse, recurrent layer known as a reservoir, wherein all incoming weights to the reservoir (including recurrent weights) are left untrained. The recurrent topology of the reservoir translates a series of inputs (and/or output feed back) into unique transients which are then read-off by a memoryless readout function. Generally speaking, since recurrent connections can lead to very complex dynamics, certain constraints are placed on the recurrent weights to prevent unstable behavior. In the case of ESNs, these constraints result in the Echo-State Property (ESP), which intuitively speaking simply states that information presented to the reservoir is asymtotically forgotten such that eventually any information concerning initial conditions are "washed out". As such, the state of the reservoir reflects a high-dimensional spatial representation of the input history over time. This allows a classifier to linearly combine information concerning a sequence of inputs through time instead of just on the most recent input.

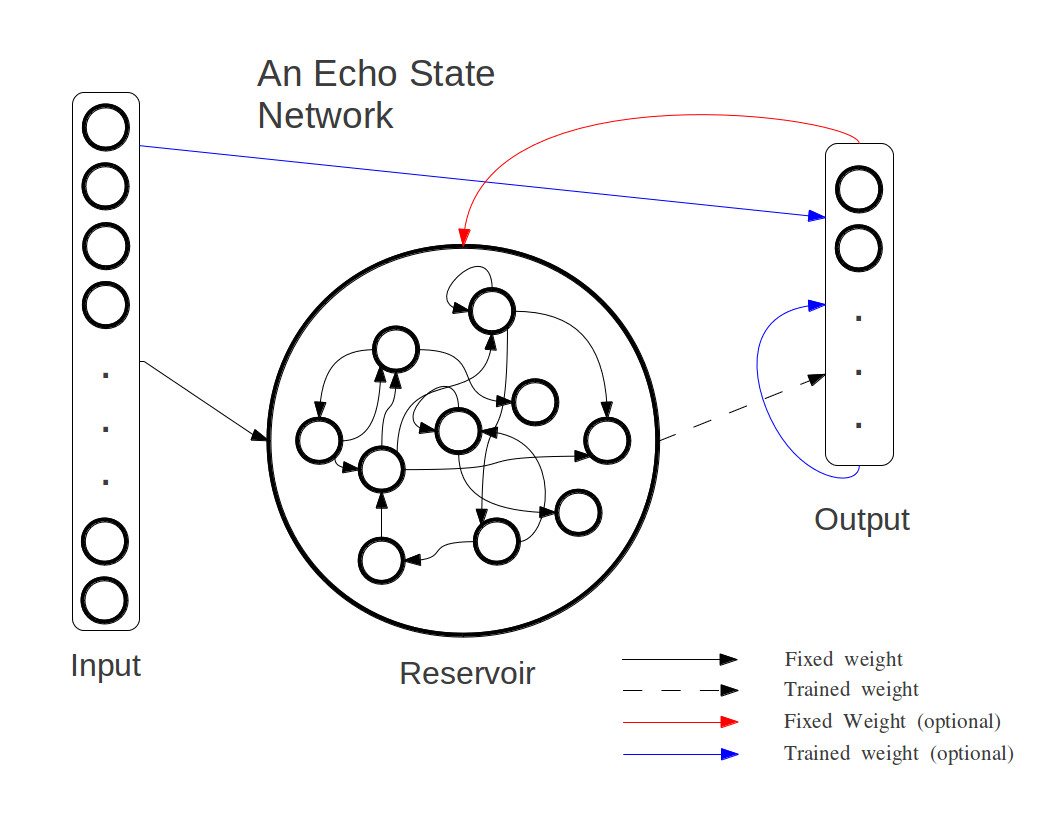
An Echo State Network

Structurally, ESNs are generally made up of sigmoidal neurons arranged into descrete input, reservoir and output layers. Training consists of collecting network states over set of input vectors and linearly combining them with a training set of expected outputs in order to form an incoming weight matrix for the output neurons. This is generally done via an offline LMS algorithm. Note that this implies that only weights to the output neurons (or read-off layer) are trained and that such weights do not actually exist prior to training. It should be noted that technically any available online or offline algorithm for linar regression can technically be used to train output weights, however as of the current version of Simbrain this is not an option, barring custom scripting.

Initialization

As with all subnetworks ESNs can be initialized through Insert > Insert Network > Echo State Network in any network window. This will bring up the ESN creation dialog.

Creation Dialog

Number of Neurons per Layer: Each layer (Input, Reservoir, and Output) has a certain number of neurons consistent with the task posed to the network. It is not advisable to have less than 50 reservoir neurons, as in practice this offers relatively poor performance.

Neuron Type: The neurons in the reservoir and output layers can have either, Linear, Tanh, or Logistic update functions. Input layer neurons are always clamped.

Connectivity Configuration: Given the diagram above, we can see that ESNs are capable of several connectivity configurations depending on the task. In all cases weights connecting the input layer to the reservoir and (after training) the reservoir layer to the output layer are necessary. Though multiple configurations are possible all configurations will essentially manifest into one of two classes of filter, either:

A finite impulse response filter (FIR): Any ESN which lacks feedback outside the reservoir (be it output-reservoir or output-output feedback) can be classified as a FIR filter. As such, any response on the part of the network to any finite length input will itself be of finite duration, that is a null input will eventually lead to a null output given enough time. This is largely a result of the ESP. Therefore any ESN lacking this form of feedback is typically suited more toward prediction tasks (where output feedback would only represent a noisy version of the input), and generalized filtering tasks.

-OR-

An infinite impulse response filter (IIR): ESNs with some form of output feedback can, in theory be IIR filters (i.e. a finite length input does not necessarily result in a decaying output signal), and tend to be better suited for modeling dynamical systems. It ought to be noted however that feedback from the output layer is more proned to instability and as can be guessed, the ESP cannot be guaranteed for such networks. Often times (depending on the task) this can be a good thing.

Connection Sparsity: These parameters simply control the overall sparsity of any untrained connections (all trained connections generally have 100% connectivity). While it was initially assumed that sparser recurrent connections within the reservoir would give rise to richer internal dynamics, studies using fully connected reservoirs have shown this to be untrue (likely due to small world properties). However, as is a key theme with ESNs such sparse connections are allowed (even between the input and the reservoir and with back-weights), and generally speaking ought to be taken advantage of in the spirit of computational efficiency.

Spectral Radius: This parameter reflects the "constraints" (though not directly, see Jaeger (2001)) mentioned earlier which prevents unstable behavior within the recurrent layer. Specifically, the ESP will be violated for all reservoirs with a recurrent weight matrix having a singular value greater than 1 for tanh neurons. However in practice setting the maximum eigenvalue of such a matrix (spectral radius), below 1 is sufficient for this condition. This has led to a misconception that the ESP is sononomous with a spectral radius below unity. In cases where the input amplitude is large, the ESP can still be guaranteed for spectral radii larger than unity. However, there is some debate in the literature over this (see Steil, 2007 and Verstraten, 2006), as spectral radii above 1 (even in cases of smaller input amplitudes) have been associated with the ESP. This implies that the spectral radii of the network may be task dependent and that spectral radii less than unity may be a sufficient, but not necessary property for the ESP.